עשרים וחמש שנים מאוחר מדי לעזור לרוס להכניס את הספה החדשה שלו לדירתו"חברים",מתמטיקאי פתר סוף סוף את "בעיית הספות" המציקה.
בעיית המתמטיקה משרטטת את הספה בגודל הגדול ביותר שיכולה להתאים מעבר לפינה ברוחב נתון - בדיוק הבעיה איתה מתמודדות הדמויות בפרק של "חברים" ששודר ב-1999. הפצרותיו של רוס מ"פיבוט!" יכול היה להימנע, מסתבר, אילו רק היה שוקל ספה של גרבר עם 18 חלקי עיקול ושטח מקסימלי של 2.2195 יחידות. (אוקיי, אז אולי זה לא היה כל כך מועיל.)
הפתרון לבעיית הספות הוא ראשון במתמטיקה. הבעיה הוצגה על ידי המתמטיקאי האוסטרי-קנדי ליאו מוזר בשנת 1966. מוסר ביקש את השטח הגדול ביותר האפשרי של צורה בודדת במישור אחד שיכול לנוע סביב פינה ישרה של מסדרון ברוחב יחידה של אחד. למרות שזה עשוי להיראות פשוט, המתמטיקה די מסובכת, מכיוון שהבעיה כרוכה גם במקסום שטח וגם בתנועה של הצורה.
עַכשָׁיו,ג'ינאון באק, חוקר פוסט-דוקטורט במתמטיקה באוניברסיטת יונסאי בדרום קוריאה, הגיע לתשובה. Baek פרסם את הפתרון שלו ב-2 בדצמבר באתר PreprintArXiv. בקצת יותר מ-100 עמודים של הוכחות מתמטיות, Baek מצא כי עבור מסדרון ברוחב של יחידה אחת, השטח המרבי של הספה הדמיונית יכול להיות 2.2195 יחידות - מה שמצמצם את התשובה בדיוק מהטווח שהיה ידוע קודם לכן של בין 2.2195 ל-2.37 יחידות. ההוכחה עדיין לא פורסמה בכתב עת בעל ביקורת עמיתים ויצטרכו לעבור אותה על ידי מתמטיקאים אחרים כדי לקבוע שהיא, אכן, אופטימלית.
קָשׁוּר:
ה"גרבר" של הספה של גרבר הוא המתמטיקאי ג'וזף גרבר, פרופסור אמריטוס באוניברסיטת רוטגרס.בשנת 1992. אבל היה ויכוח אם הספה יכולה להיות גדולה יותר, כאשר צוות בשנת 2018 השתמש בהוכחה בעזרת מחשב כדי להציע כי2.37 היה למעשה הגבול העליון.
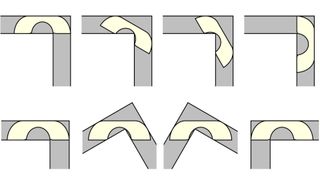
הספה של Gerver היא ספה רחבה בצורת U עם "מושב" מעוקל שיכול להידחק מעבר לפינה מבלי להיתלות. השאלה הייתה האם הספה המעוצבת בקפידה - העשויה מ-18 קימורים נפרדים ביחד - היא באמת הצורה הגדולה והאופטימלית ביותר שיכולה לעשות את הסיבוב. באק עבד על הגיאומטריה של הצורה ותנועתה ומצא שהפתרון של גרבר היה, למעשה, נכון.
ההוכחה יצרה אדווה של עניין ברשתות החברתיות.
"זו הספה האופטימלית," משתמש@morallawwithinכתב בפלטפורמה החברתית X ב-6 בדצמבר, ופרסם תמונה של צורת הספה בעלת הזרועות הדי רחבות. "אולי לא תאהבו את זה, אבל כך נראית אופטימיזציה שיא."



