מתמטיקאים הם בדרך כלל לא נקודת השיחה הראשונה ביום המעבר. ובאמת, למה הם צריכים להיות? במשך כמעט 60 שנה, הם אפילו לא יכלו לומר לך אם הספה החדשה והמפוארת שלך עם שלושה מושבים תגיע מעבר לפינה הצמודה לדירה שלך.
ג'ינאון באק פשוט עשוי לשנות את דעתנו בנושא. חובב הקומבינטוריקה והגיאומטריה מאוניברסיטת יונסאי בקוריאה ירד זה עתההוכחה של 100 עמודיםעל הבעיה הזו בדיוק, פותרים את אחת הבעיות הדוחקות ביותר של היקום כדי שכולנו נוכל לבחור ריהוט טוב יותר לפני שנתקע בראש חדר המדרגות בקומה השלישית.
בשנת 1966, המתמטיקאי האוסטרי-קנדי ליאו מוזר קבע בעיה שמטרידה את האנושות מאז מותשאוסטרלופיתיקוסעמד תחילה במקומות הרחוקים של מערה עם פגר צבי נוח למראה שפשוט לא זז יותר.
על פני השטח, זה נראה פשוט. מהו האובייקט הדו-ממדי הגדול ביותר שיכול להצליח להסתובב בפינה בצורת L?
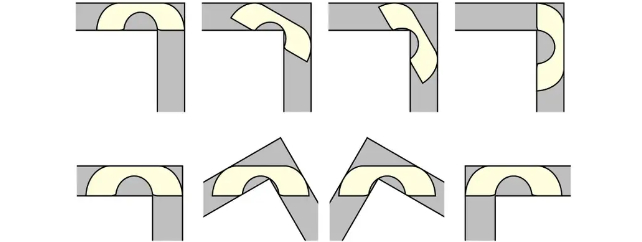
עבור מסדרון יחידה אחת לרוחבה, כיסא שהוא יחידה מרובעת אחת הוא טיול בפארק. מצד שני, יחידה מלבנית לחלוטין בת שני ריבועים תתקע כמובן. תשכחו עוד משהו - הוא חי עכשיו במסדרון.
אבל מה אם זה משהו ייחודי של איקאה שנקרא כמו דמות שר הטבעות ומעוצב כמו מקלט טלפון מיושן?
רק שנתייםלאחר שמוזר השליך את הכפפה, המתמטיקאי הבריטי ג'ון המרסלי מצא שספה המורכבת מחצי עיגול מנותח מופרדת בריבוע עם נגיסה של חצי עיגול הוסר (שבו שלושה חברים יכולים לגעת במבוכה בברכיים כשהם מדברים מתמטיקה) יכולה להיות בשטח של 2.2074 יחידות ועדיין רק לעשות את זה מעבר לפינה.
Hammersly גם סטגבול עליוןעבור העיצוב - שום דבר גדול מ-2.8284 לא יכול להידחק.
כמעט רבע מאה חלפו עד שחוקר מאוניברסיטת רוטגרס בשם ג'וזף גרבר הציע עיצוב מחדש עדין על הספה של המרסלי, עיגול כמה קצוות עם קשתות נוספות ומציאת צורה שהוסיפה שברים לגבול התחתון הקודם כדי לתבוע אתגודל הספה המקסימלי הוא שבריר מעל 2.2195 יחידות.
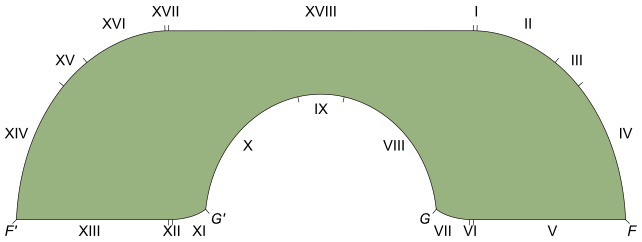
גרבר הראה בהצלחה שהפתרון שלו היה אופטימלי מבחינה מקומית, והציב גבול תחתון חדש לאזור המקסימלי. במילים אחרות, הפתרון שלו היה הטוב ביותר במסגרת התנאים המוגבלים שהוגדרו על ידי אותה צורה.
ללא נוסחה אוניברסלית לצורות ספות שמתארת את כל הממדים האפשריים של רהיטים, עם זאת, קשה להוכיח שספה קצת יותר גדולה עם קימורים שונים בתכלית עשויה לא להגיע אליה.
בשנת 2018, מתמטיקאי מכון סנטה פה, יואב קאלוס ודן רומיק מאוניברסיטת קליפורניה, דייויס השתמשו בתוכנית בעזרת מחשב כדי להראות שהספה יכולה להיות גבוהה עד 2.37 יחידות.
עבור ההוכחה האחרונה הזו, באאק יישם מעט קוסמות מתמטית הידועה בשםתפקוד הזרקהלמפות צורות מוצלחות של הספה של גרבר,נעילת מאפייני מפתח לפני שמרחיבים אותם לממדים גדולים יותר מתמיד כדי להוכיח אחת ולתמיד כמה גדולה יכולה להיות ספה דמוית גרבר.
אין ספק, 2.2195 יחידות הן מלך הספות למסדרון ברוחב יחידה אחת ולפינה בצורת L, בדיוק כפי שגרבר הציע ב-1992.
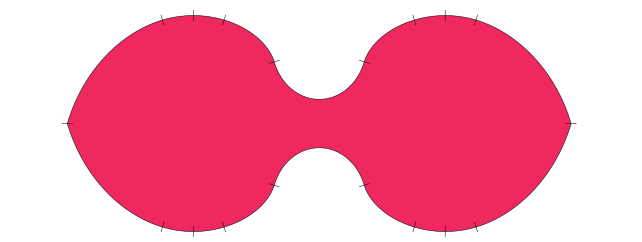
למרות שטרם זכה לביקורת עמיתים, הפתרון של Baek יכול להיות המילה האחרונה על בעיית הספה, לפחות בסביבה זו. אם יש לכם פינה שנייה לפנות בכיוון ההפוך, אנו ממליצים על צורה הנקראת ספה דו-ביתית של רומיק.
זמין כעת במעבר 13 באיקאה, ליד שולחן המטבח של גימלי.
מחקר זה זמין בשרת הטרום-פרסוםarXiv.






